Morphomatic

The metric circle geometry has to do with the metric properties of structures that has circles as basic objects. Of these structures there are some only concerning the relations of the radiuses of the circles. Then there is also a very fundamental type that has to do with a kind of distance between circles, and from this theorems can be developed almost endlessly.

Of the radius theorems we shall consider two types, one that is connected to the apollonius circles, and one that is connencted to the Hart circle theorem. Then we will look at the general type.

The apollonius metric theorem

The metric solution of the apollonius problem is quite complex, and it has been considered from many viewpoints. We discuss this nearer elsewhere, and brings here the formula of the radius of an apollonius circle given the inverse radiuses of the three other circles, and the distangles between them.

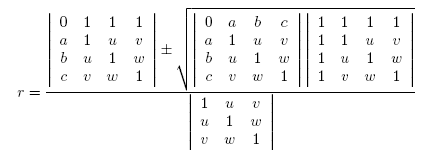
There are eight solutions to the apollonius problem in the general case, and the above formula gives two of them. When we add the two solutions, the square root expression is falling, and we get as sum a fraction of two determinants. This sum is a linear relation. The other three pairs of apollonius circles gives rise to similar formulas, and a combination of all four, gives a simple relation among all eight inverse radiuses. There must be taken consideration of how the sign of the radiuses are. We say that the tangency between two circles is negative if they touch each other outwardly, and positive if the one is inside the other. The sign of an apollonius circle is defined as the product of the three tangencies. Then we have the relation.

Theorem: Taking into account the sign of the radiuses of the apollonius circles, the sum of the eight inverse radiuses of the is zero.

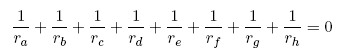
The theorem can be tried here: Eight apollonius circles.

From this theorem several can be deduced, and some of the species are developed here: