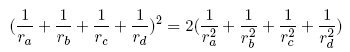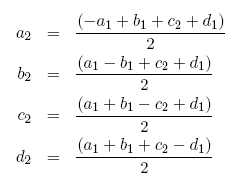Morphomatic

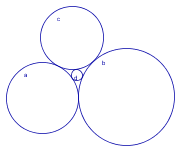
The most famous metric circle theorems is the Descartes theorem. The geometric structure is four circles that are all tangent to each other. If the radiuses of three of the circles are known, the fourth can be calculated. One can use several methods to accomplish this, and through times several mathematicians has solved the problem. Among these are Descartes, Jacob Steiner and Soddy. They solved the problem independently of each other, so the theorem has had several names.

The solution of the problem is most often put in the following way.

Theorem: The square of the sum of the bends, is equal to twice the sum of the squares of the bends.

The bend of the circle is defined to be the inverse radius.

Form this formula the radius of one of the circle can be calculated given the four other.

The formula can be calculated in many ways. In this treatise the procedure of Jacob Steiner, the vector method, and the determinant method is described. The determinant method is the morphological way.

As we see from the expression of the relation between the circles, the inverse radius is the central quantity. From now on we use this in the expressions, and will call the four inverse radiuses a, b, c and d. Then the formula above will have the form

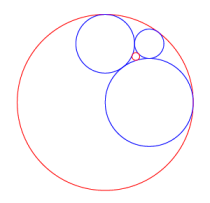
The Descartes formation is in one sense complete, but the four circles are related with four other circles that adds many new features.

The two solutions

When we solve the equation above with request on one of the variables, we get two solutions.

The two solutions represents the two ways a circle can touch three other that are tangent to each other. The sum of the solutions is

The twin circles

The four circles that comes into play in addition to the four Descartes circles, are the circles that are orthogonal to each three of the original circles. The remarkable thing appear, that these circles also make a Descartes formation. And the orthogonal circles to these four, are the original circle. So there is a complete symmetry between the two pairs of four circles.

From this follow that also the four orthogonal circle are connected by the same formula. In addition there are several other arithmetical relations between the eight circles. One important property is that the values of the eight inverse radiuses make a twin number relation. We discuss such numbers on another page (Twin quadruples), and only define them short here. If we have four numbers a₁, b₁, c₁ and d₁, then there are four other numbers a₂, b₂, c₂ and d₂, defined by

The first such relation is the connection between three of the Descartes circles and their orthogonal circle. Her the relation is:

Theorem: Given three circles that is tangent to each other,and the circle orthogonal to these three. The the iraduses are ralated by the formula.