Morphomatic

When one of the circles in the fore-circle type becomes a line, the formulas of the structures are simplified. However, the general formula is still large.

Given three circles with iradiuses a, b and c, with distangles u, v and w, and a line that has distangles p, q and r to the circles. Then the relation between the variables is given by:
- a² + a²r² + a²w² - 2a²qrw + a²q² + 2abu - 2abr²u - 2acuw + 2acqru - 2abvw + 2abqrv + 2acv - 2acq²v + 2abprw - 2abpq - 2acpr + 2acpqw - b² + b²r² + 2bcw - 2bcqr + b²v² - 2b²prv - 2bcuv + 2bcpqv + b²p² + 2bcpru - 2bcp²w - c² + c²q² + c²u² - 2c²pqu + c²p² = 0

When tangency and orthogonal relations occur, the formulas are greatly simplified. In many cases the situation can then be calculated straight forwards by Euclidean means. The most easy case we have when one of the circles in the orthogonal theorem becomes a line. Then the situation is:

Given two circles tangent to a line, and a circle orthogonal to these circles, and to the line. What is the relation of the radiuses of the circles?

This is the same as finding the distance between the points of tangency. , and it can be done by using the Pythagorean theorem.

The Descartes theorem when one circle is a line can be calculated by using the above theorem three times.

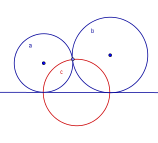
The orthogonal species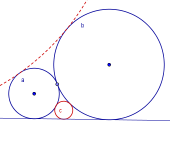

The Descartes when
one circle is a line.