Apollonius gasket
One very special formation of integer circle relations, is what is called the apollonius gasket. This structure starts with a Descartes integer formation, In this formation four circles all tangent to each other all have integer inverse radius. Then any circle tangent to any three of these, also has integer inverse radius. This also continues, as the circle tangent to any new triple tangent to each other, also integer inverse radius. The circles get smaller and smaller; the inverse radiuses always has integer values, this value increases. An explanation of this phenomena we find in the 2. Descartes theorem. Theorem: Given three circles a, b c tangent to each other, and two circles d and e tangent to the three. Then the relation of the radiuses of the circles are given by:
If the expression of the inverse radiuses are the same as the circles we get:
Given a Descartes formation, we can then from this relation calculate the polar apollonius circle, and when the other inverse radiuses are integer, then the polar also has to be so. |
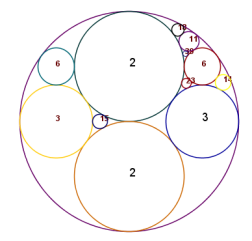
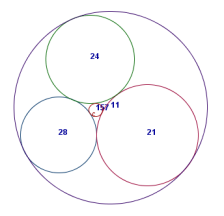
|
Demonstration
| In the exercise new circles appear when four circles that all touch each other are clicked when we first have activated the macro icon. The new cicle will then toutch the first three, and will be opposite of the fourth cicle cliked. We calculate the inverse radius of the new circle bay adding the inverse radius of the three circles, multiplying by two, and subtract the polar circle. If th epolar circle is the circumcircle, then the inverse radius of this is added. The prosess can go on; we can enlarge the picture when the enlarge icon is clicked. |